今天要來介紹一個非常重要的結構：Binary Tree。昨天說到，他可以最大化減少 Linking space 的浪費問題

何謂二元樹？

二元樹的定義為：
可為空樹，若非空樹，則：

1. 具有樹根（root）及左子樹（Left subtree）、右子樹（Right subtree）
2. 樹根之左右子樹皆為二元樹

二元樹是不是樹？

答案是：二元樹不是樹！二元樹雖然有樹的結構特徵，但與一般的樹有顯著差異。

我們用個比較表來說明：

因此嚴格上來說：二元樹並不是樹。

Binary Tree 的種類：

1. 斜曲樹（skewed Binary tree）

每個節點皆只有左子樹（left skewed tree），或只有右子樹（right skewed tree）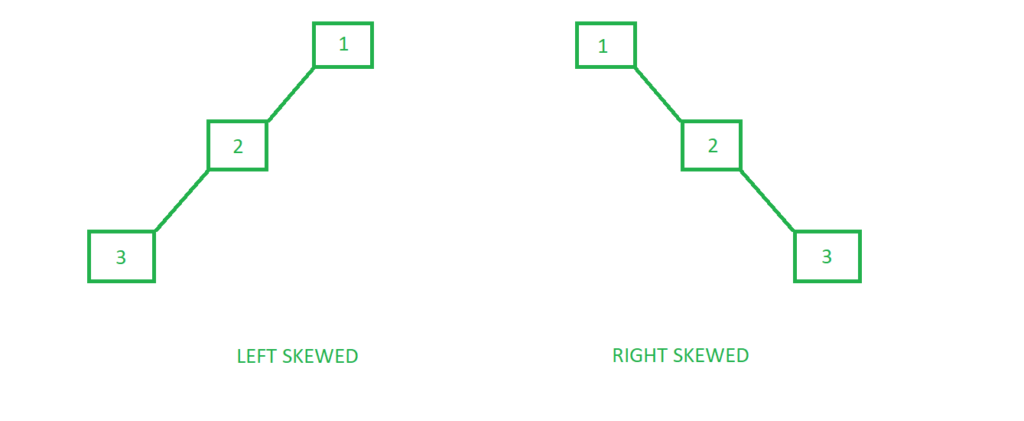

2. 完整二元樹（Complete Binary tree）

這個結構相當重要，到後面的高等樹還會常常看到他。
Complete Binary Tree 的定義為：不同 level 由上而下生長，同個 level 是由左至右生長
來看個圖片：

可以看到在同一個 level 中，是從左邊往右邊長，並且一個 level 長完才長到下一個 level。
如果將每個節點編號的話，root 編 1 號。則：

1. 若某點編號為 i，其左子節點編號為 2 * i，其中右子節點編號為 2 * i + 1。（前提是其子點要存在）
2. 若某點編號為 i，其父節點編號為 [i / 2]（[]為向下取整樹。前提也是其父點要存在）

以上面那棵樹為例：A 為 1 號，B 為 A 之左子點，編號：2 * 1 = 2

3. 滿枝二元樹（Full Binary Tree, Perfect Binary Tree）

如果此樹的高度為 H，則此樹擁有這個高度可能的所有節點。

4. 嚴格二元樹（Strict Binary Tree）

嚴格二元樹指，所有的節點 degree 皆為 0 或 2
也就是說：非樹葉節點的分支度皆為 2

不過有些版本是將它稱為 Full Binary Tree。

二元樹三大定理（此假設 root level = 1）

前兩個定理皆跟 Full Binary Tree 相關，可以參考剛剛的圖

定理一：level i 的 Nodes 最多有 2^(i-1) 個

可以利用數學歸納法來證明：

1. 當 i = 1 時，level 1 節點有 2^(1-1) = 1 個，此點為樹根，初值成立
2. 假設 i = K 時，level K 的節點最多有 2^(K - 1)個成立
3. 當 i = K + 1 時，因為求的是最多節點，代表所有父節點（位於 level K）皆產出兩個子節點。
   因此 level K + 1 的點共有 2^(K - 1) * 2 = 2 ^ K = 2 ^ ((K + 1) - 1) 成立
4. 由數學歸納法得證

那如果是level i 的最少節點數呢？
不用想吧，就是 1。

定理二：若樹高為 H，則此棵樹的節點總數最多為2^H - 1

一樣利用數學歸納法來證明：

1. 當 H = 1 時，節點最多有 2^1 - 1 = 2 - 1 = 1 個，此點為樹根，初值成立
2. 假設 H = K 時，節點最多有 2^K - 1 個成立
3. 當 H = K + 1 時，因為求的是最多節點數，因此高度為 K + 1 的樹就是就是將高度為 K 的樹之節點總數，加上 level K + 1 的最多節點樹。再由定理一得知，level K + 1 的節點最多有 2^K 個。
   因此高度為 K + 1 的樹最多有 2^K - 1 + 2^K = 2^(K + 1) - 1 個節點，成立。
4. 由數學歸納法得證

如果是高度為 H 的節點總數最少值呢？答案就是 H。每個 level 只有一顆節點，也就是 Skewed Tree。

定理三：若一顆樹之樹葉節點有 N0 個，分支度為 2 之節點有 N2 個，則 N0 = N2 + 1

這個定理的證明相當有趣。
假設 N 為節點總數，再另 N1 為分支度為 1 的節點個數。
則推導出：N = N0 + N1 + N2

再來 另 B 為樹的分支總數，或稱為鏈結總數。
則可以推導出兩式：

1. B = N - 1。因為除了樹根沒有之外，每個節點皆被一個鏈結連接。
2. B = 0 * N0 + 1 * N1 + 2 * N2。因為分支度 0 的節點創造 0 個鏈結，分支度為 1 的節點創造 1 條鏈結，分支度為 2 的節點創造 2 支鏈結。

整理上面式子：(N0 + N1 + N2) - 1 = N1 + 2 * N2
即可得出 N0 = N2 + 1

二元樹的表示方法（representation）

Array Method

分成兩個 case：

1. 若 Binary Tree 不是 Complete Binary Tree，則準備：2^H - 1 個空間的 Array， H 為此樹之樹高。
   再來按照 Complete Binary Tree 的編號方式幫節點編號，空值編號及留空。
2. 若 BinaryTree is Complete Binary Tree，則準備：H 格空間，並依照編號充分運用。

優點：容易存取父點（因為 Array 的 Random Access 特性），且若樹為完整二元樹，不會浪費空間。
缺點：因 Array 需固定長度，增刪節點較困難。若樹為 skewed tree，則很浪費空間（2^H - 1 - H 格）

Linked List Method

定義節點結構：一格放 data，一格放指標指向 left child 節點，再一格放指標指向 right child 節點

優點：若樹為斜曲，則較 Array 不浪費空間。增刪節點也較方便。
缺點：parent 難存取（使用的是單向鏈結）。平均來說較浪費空間（浪費 N + 1 個 link）

總結

若樹為完整二元樹（如：heap），我們會使用 Array 來表示二元樹，其他狀況基本上都是使用 Linked List 法。

今天介紹了二元樹還有定理。明天我們要來看二元樹的走訪，以及好久不見的遞迴如何用在二元樹的操作上！

參考資料：

1. https://www.geeksforgeeks.org/skewed-binary-tree/
2. https://www.geeksforgeeks.org/complete-binary-tree/
3. https://www.geeksforgeeks.org/perfect-binary-tree/
4. https://faculty.cs.niu.edu/~mcmahon/CS241/Notes/Data_Structures/binary_trees.html#:~:text=If%20every%20non-leaf%20node,always%20contains%202N%20-%201%20nodes.